Modern Robotics, Course1 / Chapter 2

---

2.1 Degrees of Freedom of a Rigid Body (강체의 자유도)

로봇을 다룰 때 필요한 가장 기초는 ‘로봇이 어디에 있는가?’입니다. 이때 필요한 것이 로봇의 위치(Configuration)이죠.
이 강의에서는 로봇의 몸체가 단단한 물체(강체, rigid body)인 상태에 대해서만 살펴봅니다.
이 로봇의 몸체를 link라 부르는데 link는 나무토막처럼 일정한 형태를 갖기에 몇개의 숫자로 위치를 표현할 수 있습니다.

로봇의 가능한 모든 위치를 포함하는 n차원 공간을 Configuration Space (C-space)라고 합니다.
dof(degrees of freedom)는 C-space의 차원이라고 할 수 있고, 로봇의 위치를 표현하기 위해 필요한 숫자의 갯수라고도 할 수 있습니다.

책의 p.32 Figure 2.1을 보면
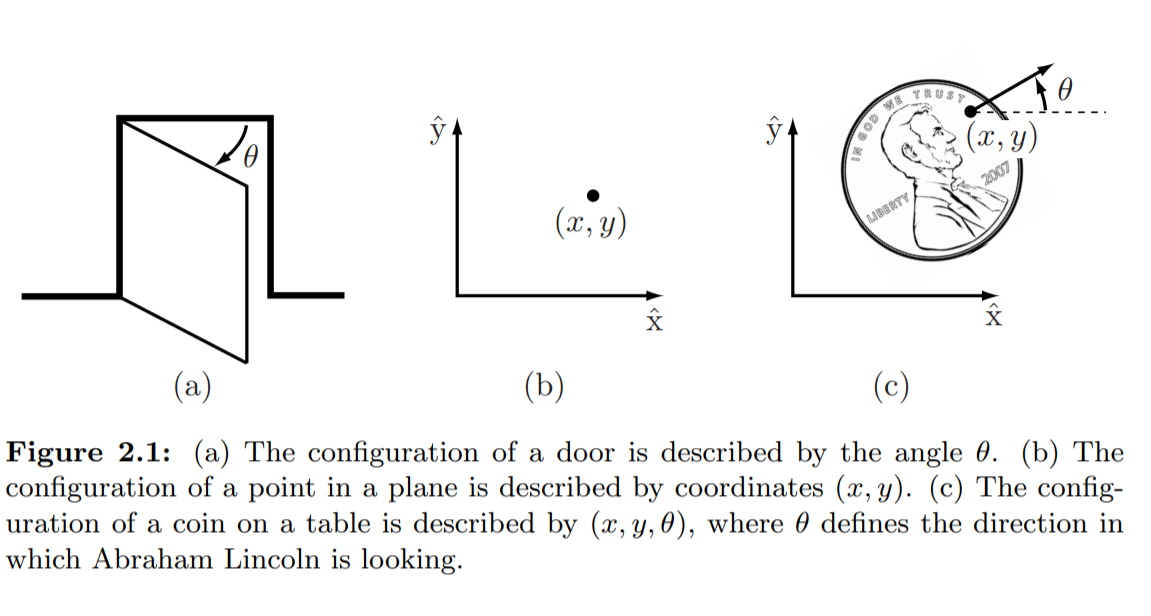(a)의 문은 그 위치를 표현하기 위해 경첩을 기준으로 얼마나 회전했는지에 대한 각도인 Φ 1개만 있으면 됩니다.
(b)의 점은 평면 상의 점이므로 점의 좌표인 x, y 2개의 값으로 위치를 표현할 수 있습니다.
(c)의 동전은 동전위의 한 점의 x,y 좌표와 동전이 기울어진 정도 (각도) 3개의 값으로 위치를 표현할 수 있습니다.

Figure 2.2를 통해 강체의 자유도를 알아봅시다. 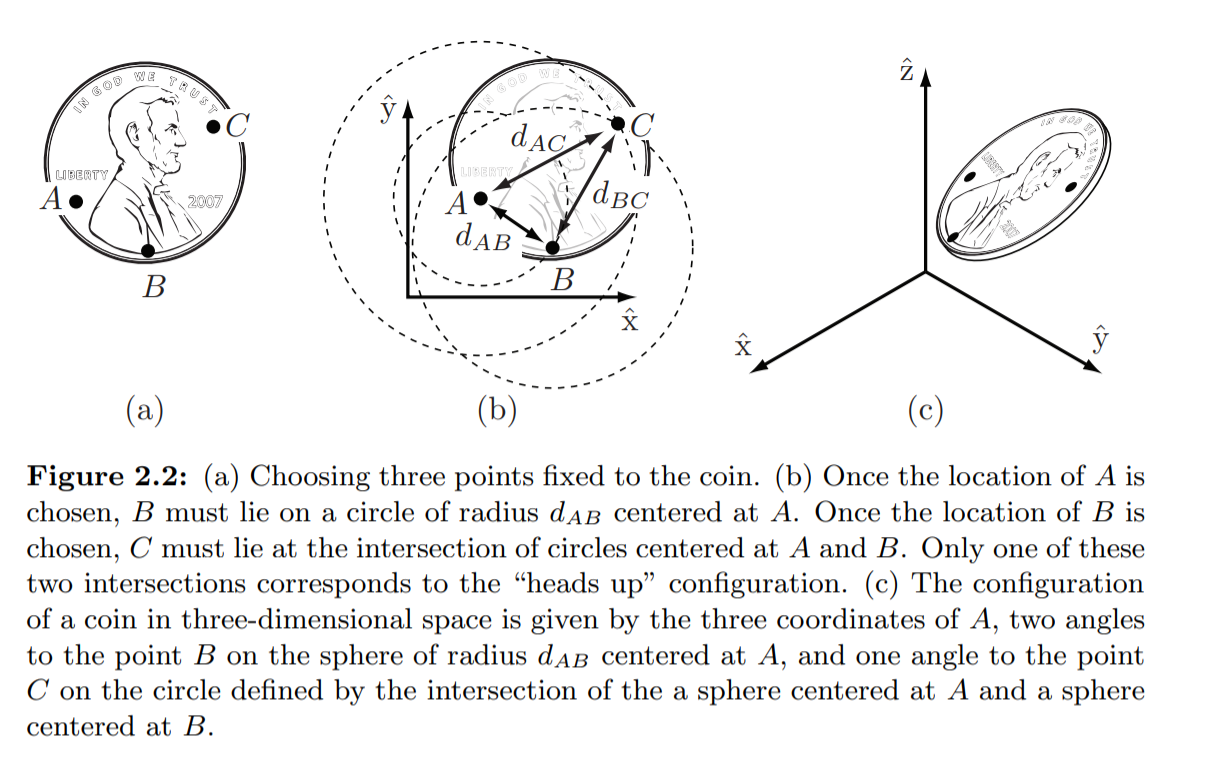(b)에서 점 A, B, C는 모두 각각 2개의 좌표(값)로 표현가능합니다. {(x_A, y_A), (x_B, y_B), (x_C, y_C)}
6개의 임의의 값(독립적인 값, independent)으로 동전의 위치를 정할 수 있으면 이는 6의 dof를 갖는 것입니다.
하지만 동전은 강체(rigid)이므로 A가 정해지면 A,B 간의 거리d(A, B)가 일정함에 의해 B의 위치가 제한(constraint)됩니다.
그 위치는 A를 중심으로 하고 반지름의 d_AB인 원 위이죠.
이때 B의 위치는 Φ_AB(AB벡터와 x축 벡터가 이루는 각)하나로 표현이 가능합니다.
이후 점 C의 위치는 원AC, 원BC의 두 교점에서 가능한데, 이는 동전의 앞, 뒤에 따른 것이므로 사전에 동전의 면을 지정하면 C의 위치는 명백해집니다(C is fixed).
따라서 동전의 평면에서의 위치(configuration)는 (x_A, y_A, Φ_AB) 이렇게 표현이 가능하고 3의 dof를 갖는다는 걸 알 수 있습니다.

이 예를 일반적인 규칙으로 적용하면 dof에 대한 공식을 얻습니다.(식 2.1)

dof = 지점들의 자유도의 합 - 제한들(constraints)의 갯수

위의 예를 적용시켜보면 동전 위 지점들의 자유도 합은 A, B, C 모두 x, y값을 가지므로 2+2+2 = 6의 자유도를 갖습니다.
한편 A가 정해지면 B는 A에 의해 d(A,B)라는 1개의 constraint가 생기고, 마찬가지로 C는 A, B에 의해 2개의 constraints가 생깁니다.
따라서 1+2 = 3의 constraints(제한)이 있어 평면 위 동전의 자유도(dof)는 6-3 = 3이 되는 것입니다.

이를 확장해 3차원 공간에서 동전의 위치를 생각해봅시다.(Figure 2.2(c))
점 A, B, C는 모두 x,y,z좌표를 가질 수 있으므로 총 9의 자유도를 가집니다.
한편 A가 정해지면 B는 A에 의해 1개의 constraint를 갖고, C는 A, B에 의해 2개의 constraints를 갖게 되므로 3차원 공간에서 동전의 dof는 9 - 3 = 6이 됩니다.
같은 예를 조금 다르게 살펴보면 점 A는 x,y,z 좌표를 자유롭게 선택 가능해 3의 자유도를 가집니다.
점 B도 x,y,z 좌표로 표현이 가능하나 A로 인한 1개의 constraint를 가지기 때문에 B는 3-1=2의 자유도를 가진다고 할 수 있습니다.
마찬가지로 점 C도 x,y,z 좌표를 가지지만 2개의 constraints를 갖기 때문에 C는 3-2=1의 자유도를 가집니다. 따라서 3차원 공간 위 동전의 자유도는 3+2+1=6이라고 할 수 있습니다.

---

2.2 Degrees of Freedom of a Robot (로봇의 자유도)

로봇은 몸체인 link와 관절인 joint로 구성되어 있습니다.

Figure 2.1(a)의 문을 다시 살펴봅시다.
우리는 문의 위치를 θ만으로 표현할 수 있어 문의 자유도가 1이라는 것을 알고 있습니다.
경첩이 없었다면 문은 3차원 공간상에 자유롭게 위치할 수 있어 6의 자유도를 가질 것입니다.
(a)의 상태를 문이라는 강체(body, link)가 경첩이라는 joint에 의해 벽과 연결되어 있기 때문에 5개의 constraint가 생겨 1의 자유도만 남았다고 볼 수 있습니다.

위의 예시에서 알 수 있듯 joint는 강체(rigid body)의 행동에 제약(constraint)을 가합니다.
이런 관점에서 joint의 갯수를 통해 로봇의 dof를 알아내는 공식인 Grubler’s formula를 도출해낼 수 있습니다.

2.2.1 Robot Joints

Figure 2.3은 로봇의 기본적인 Joint들입니다.

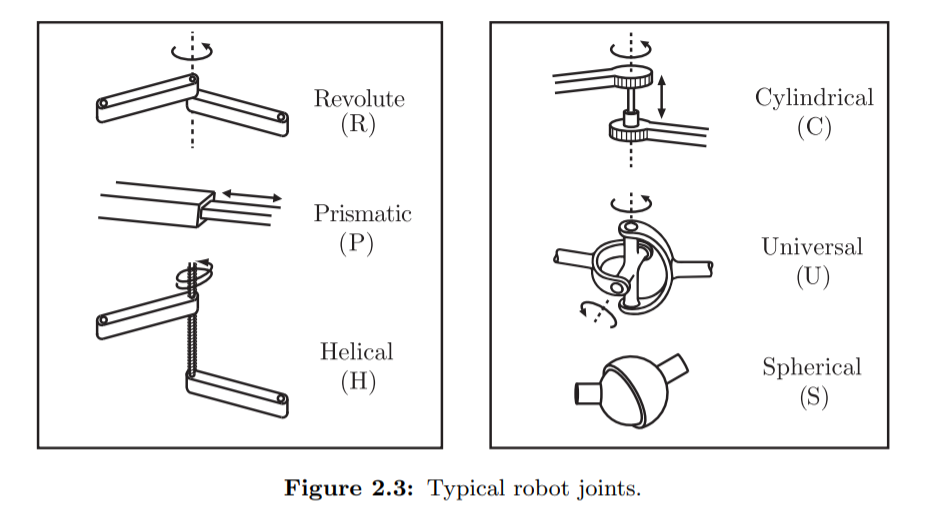
로봇의 Joint는 ‘두개’의 link를 연결합니다.(3개 이상의 link를 연결하는 것은 허용되지 않습니다.)

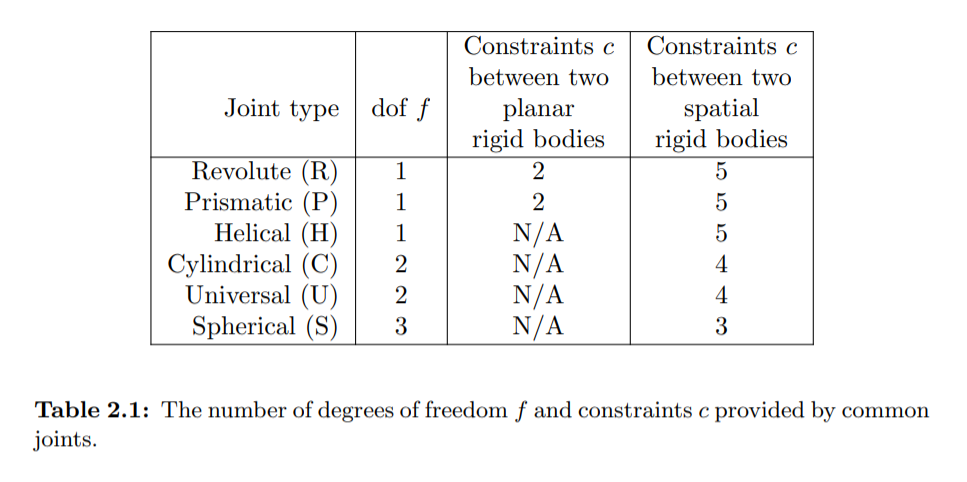
Table 2.1은 각 Joint들의 dof를 정리한 표입니다.

2.2.2 Grubler’s Formula

Grubler’s Formula는 로봇의 dof를 구하는 공식으로 다음에서와 같습니다.(식 2.4)

m = 몸체의 dof 수 (평면 : 3, 공간 : 6)
N = 로봇의 link 갯수 (ground 도 link로 친다.)
c_i = i번째 Joint의 constraint 수
J = 로봇의 Joint 갯수
f_i = i번째 Joint의 자유도(freedom)

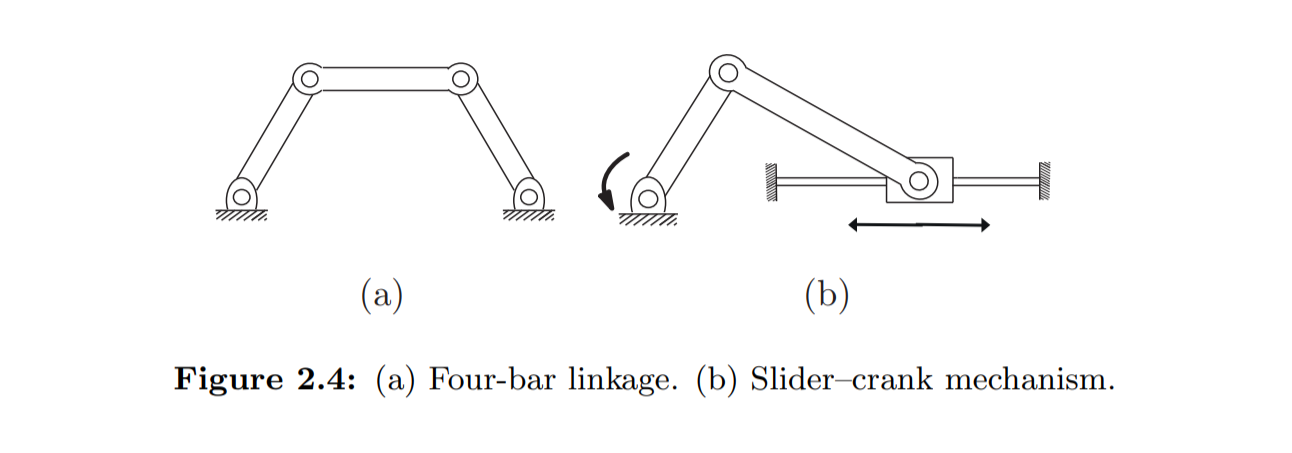
Figure 2.4(a)는 4개의 link(몸체)를 가지고(ground 포함) 4개의 revolute joint(회전 관절)를 가집니다.
모든 link가 같은 평면 상에서 움직이므로 m = 3입니다.
N = 4, J = 4, f_i = 1, i = 1,…,4를 Grubler’s formula에 대입하면 (a)는 1의 dof를 갖는다는걸 알 수 있습니다.

(b)는 두가지 방법으로 해석이 가능합니다.

1. 해당 매커니즘은 3개의 revolute joint와 1개의 prismatic joint를 가지고(J = 4, 각 f_i = 1) 4개의 link로 구성되어 있다(N = 4, ground link 포함),

2. 매커니즘은 2개의 revolute joint (f_i = 1)와 1개의 RP joint(revolute and prismatic joint의 약자, f_i = 2)를 가지고 3개의 link로 이루어져있다(N = 3; 각 joint는 2개의 link만을 연결해야 하기 때문).

두가지 방법 모두에서 메커니즘은 1의 dof를 가진다.

---

2.3 Configuration Space : Topology and Representation

2.3.1 Configuration Space Topology

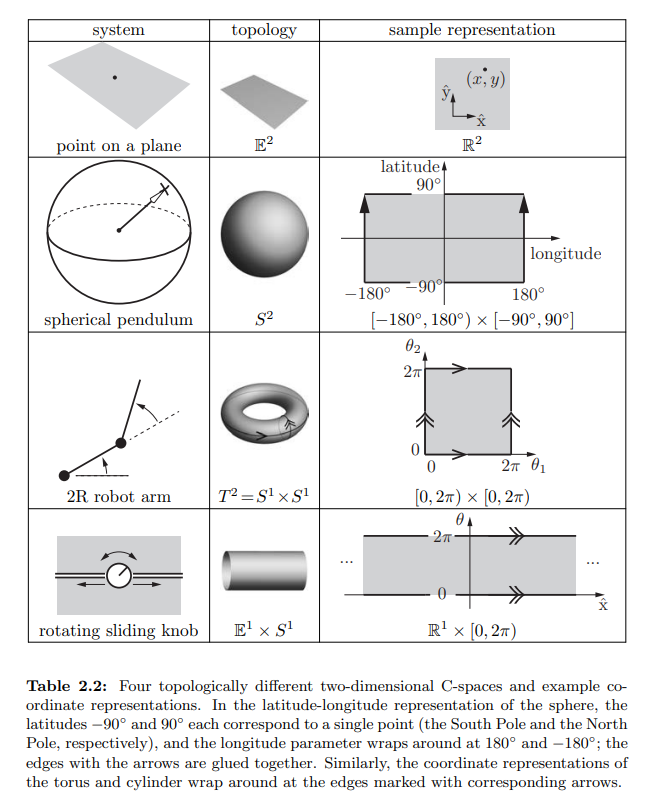
로봇의 C-space에서 dof만큼 중요한 것이 그 공간의 모양(shape)입니다.

구의 표면 위에 있는 점을 생각해 봅시다.
이 점을 표현하기 위해서는 두개의 좌표가 필요합니다.(경도, 위도)
이번에는 평면(plane) 위에 있는 점을 생각해 봅시다.
역시 마찬가지로 두개의 좌표(x,y)로 점의 위치를 표현할 수 있습니다.

구의 표면과 평면은 모두 2차원 C-space이지만 두 공간의 모습은 다르다는걸 알고 계실겁니다.
여기서 공간의 모습이 다르다는 말은 서로 위상동형(Topologically equivalent)이 아니다라는 뜻입니다.
구와 럭비공처럼 자르거나 붙이지 않고 부드럽게 구부리고 늘이는 것으로 다른 형태를 만들 수 있으면 위상동형(Topologically equivalent)이라고 할 수 있습니다.

위상적으로 구분되는(Topologically distinct) 1차원 공간으로는 원, 직선, 닫힌 구간의 선분이 있습니다.
원은 S 또는 S¹라고 표기하며 1차원의 구(Sphere)라는 뜻입니다.
직선은 E 또는 E¹라고 표기하며 1차원의 유클리드 공간(Euclidean space)라는 뜻입니다.
보통 직선의 점은 실수(Real number)로 표현되기에 R 또는 R¹으로 대신 표기하기도 합니다.

높은 차원에서 Rⁿ은 n차원 유클리드 공간이고 Sⁿ은 n+1차원에 있는 구의 n차원 공간이라고 할 수 있습니다.
S²는 3차원에 존재하는 구의 2차원 표면인 것처럼요.

여기서 알아야 할 중요한 점은 공간의 위상(Topology of Space) 은 공간 위에 있는 점을 어떻게 표현하는가와 관련없는 근본적인 속성(fundamental property) 이라는 것입니다.

예를 들어 원(circle) 위의 점을 표현할 때 원 중심과 기준점으로부터의 각 θ를 사용할 수도 있지만 좌표축을 정해 x²+y²=1 을 만족하는 (x,y)좌표를 사용할 수도 있습니다.
하지만 어떻게 표현을 하던지간에 원의 모양은(공간은) 변하지 않습니다.

어떤 C-space는 두개 이상의 낮은 차원의 데카르트 곱(Cartesian product) 으로 표현이 가능합니다.

예를 들어

• 평면에 존재하는 강체(rigid body)의 C-space는 R² × S¹으로 표현이 가능합니다.
  여기서 R²는 위치 정보인 (x,y)좌표의 공간, S¹은 각 θ의 공간을 뜻합니다. (Figure 2.2 (b) 참고)

• 2R 로봇의 C-space는 S¹ × S¹ = T².

  Tⁿ 은 n+1차원 공간에 존재하는 도넛(Torus)모양의 n차원 표면입니다. 구(Sphere)와 도넛(Torus)은 위상동형(Topologically equivalent)아니기 때문에
  S¹ × S¹ = S² 가 아니라 T² 이 됩니다.

• 2R 로봇 팔을 단 평면 상의 강체의 C-space는 R² × S¹ × T² = R² × T³.

• 3차원 공간에서 강체의 C-space는 dof를 구했을 때를 참고하면 (x,y,z)좌표의 R³, 구 표면 위치인 S², 윈 위의 위치인 S¹ 을 종합하면 됩니다.
  따라서 3차원 공간에서 강체의 C-space는 R² × S² × S¹.
  
  

2.3.2 Configuration Space Representation

계산을 하기 위해선 공간의 수치표현(numerical representation) 이 필요합니다.

공간을 수치로 표현할 때 기준 좌표축은 어떻게 설정할 것인지, 길이의 단위는 뭘로 할 것인지 등의 선택이 들어가기 때문에 표현된 수치는 공간의 Topology만큼 근본적이지 않습니다.

공간을 표현하는 방법으로는 explicit parameterization과 implicit parameterization이 있습니다.

• explicit parameterization은 n차원의 공간을 표현할 때 n개의 parameter를 사용하는 방법입니다.
  예를 들어 구 표면을 표현하기 위해 경도, 위도 2개의 값을 사용하는 방식이 이에 해당합니다.
  이 방식은 최소한의 숫자로 공간을 표현할 수 있다는 장점이 있지만, 북극점이나 남극점에서는 조금만 움직여도 경도가 아주 크게 변해버리는 특이점(singularity) 이 존재한다는 단점이 있습니다.

• implicit parameterization은 n차원의 공간을 표현할 때 n+1개의 parameter를 사용하는 방법입니다.
  구 표면을 표현하기 위해 3차원 좌표(x,y,z)를 사용하는 방식이 이에 해당합니다.
  이 방식은 특이점이 없다는 장점이 있지만 parameter가 많아진다는 단점을 갖고 있습니다.
  
  

---

2.4 Configuration and velocity constraints

closed-loops를 가진 로봇들은 implicit한 표현을 explicit한 표현보다 쉽게 얻을 수 있습니다.

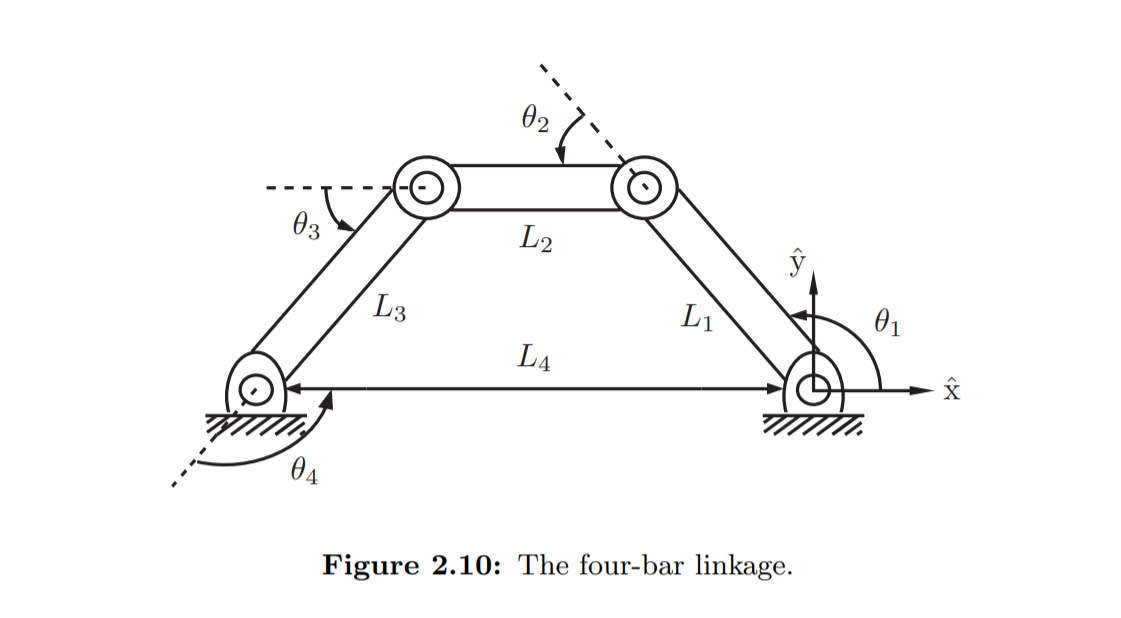
Figure 2.10에서 다음 3개의 방정식을 쓸 수 있습니다.

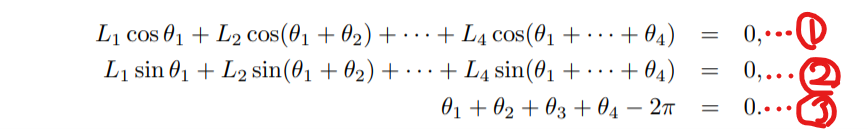
①은 link의 위치에 관한 식입니다.

• L₁에서 L₂, L₃, L₄를 거쳤을 때 원점에 도달함을 나타낸 식입니다.

②는 L₄의 방향에 관한 식입니다.

• L₄의 가리키는 방향이 L₁의 시작지점과 일치함을 나타낸 식입니다.

③은 closed-loop에 관한 식입니다.

이러한 방정식을 loop-closure equation 이라고 합니다.

한개 이상의 closed-loop를 갖는 일반적인 로봇의 C-space는 implicit하게 열벡터 θ = [θ₁, θ₂, ···, θ₄]^T 로 표현됩니다.
이 로봇은 다음의 loop-closure equation을 갖습니다.

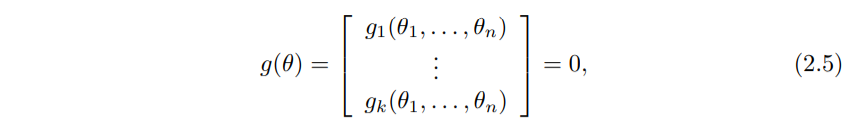
(각 식은 서로 독립이고, k ≤ n)

로봇이 움직일때를 살펴봅시다.

g(θ) = 0 을 시간에 대해 미분하면 (식 2.6)을 얻을 수 있습니다.
마지막 식은 이를 행렬의 곱의 형태로 나타낸 것입니다.

이 식을 다시 (식 2.7)처럼 쓸 수 있고, (식 2.8)의 형태는 Pfaffian constraints form이라고 합니다.

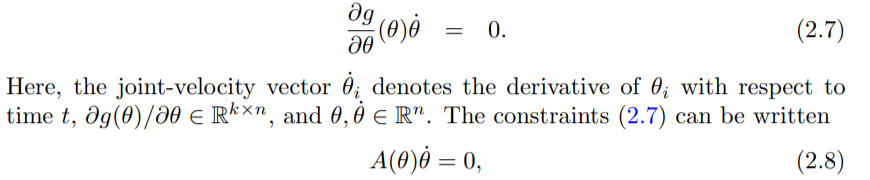
(식 2.5)는 로봇의 C-space를 제한하는 constraint(위치에 대한 제약)라서 C-space의 차원을 낮춥니다.
이러한 constraint를 holonomic constraint라고 합니다.

(식 2.7, 2.8)에서 g(θ)는 A(θ)를 적분해 얻을 수 있습니다.
따라서 g(θ) = 0 형태의 holonomic constraints는 integrable constraint라고 합니다.

(식 2.7)은 로봇이 움직일 때에 관한 식이므로 로봇의 속도의 제약(velocity constraint) 에 관한 식입니다.

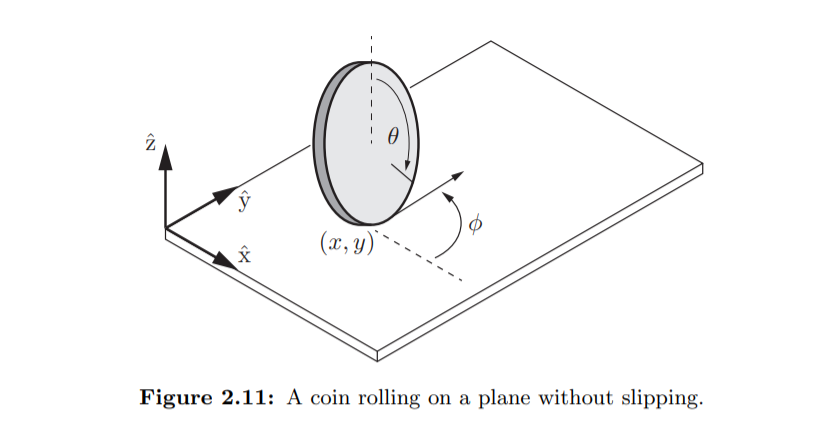
Figure 2.11에서
동전의 반지름 = r
동전이 평면과 만나는 지점 : (x, y)
동전이 구른(회전한) 정도 : θ
동전이 굴러가는 방향(steering angle) : Φ

위의 조건들로 인해 동전의 속도는 다음 방정식들을 만족해야 합니다.

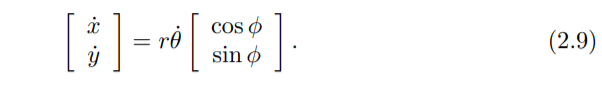
(좌변 행렬의 항은 각각 x, y의 속도)

벡터 q를 사용하면 (식 2.10)을 얻을 수 있습니다.

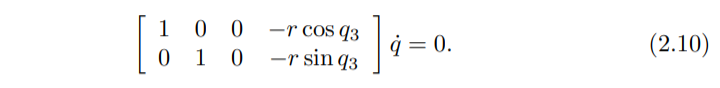
이 식을 pfaffian form으로 쓰면 다음처럼 쓸 수 있습니다.

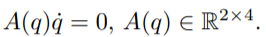
(식 2.10)은 적분이 불가능합니다.
이러한 constraint를 nonintegrable하다고 하고, nonintegrable constraint를 nonholonomic constraint라고 합니다.

이러한 constraint (nonholonomic constraint)는 속도에 대한 제약이기에 속도에 대한 차원을 낮추지만 C-space의 차원을 낮추진 않는다. (Such constraints reduce the dimension of the feasible velocities of the system but do not reduce the dimension of the reachable C-space)

---

2.5 Task Space and Workspace

-Task Space : 로봇과 관계없이 Task를 수행할 수 있는 공간.

• 종이에 점을 찍는 작업의 Task Space는 R²
  
  

-Work Space : 로봇의 작용점(end-effector)이 미칠 수 있는(닿을 수 있는) 공간.

• 로봇의 작업(task)에 관련없이 로봇의 구조와 관련있다.
  
  

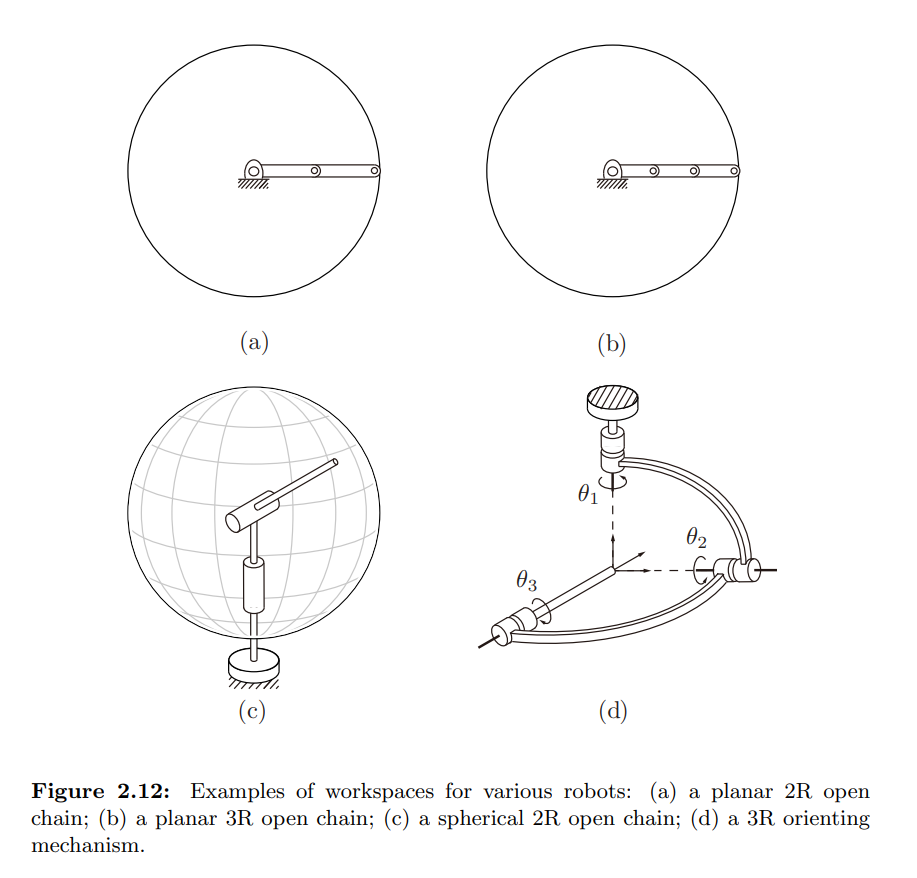
다양한 로봇의 workspace.