Modern Robotics, Course1 / Chapter 3
3.1 Rigid-Body Motions in the Plane (평면에서 강체의 움직임)
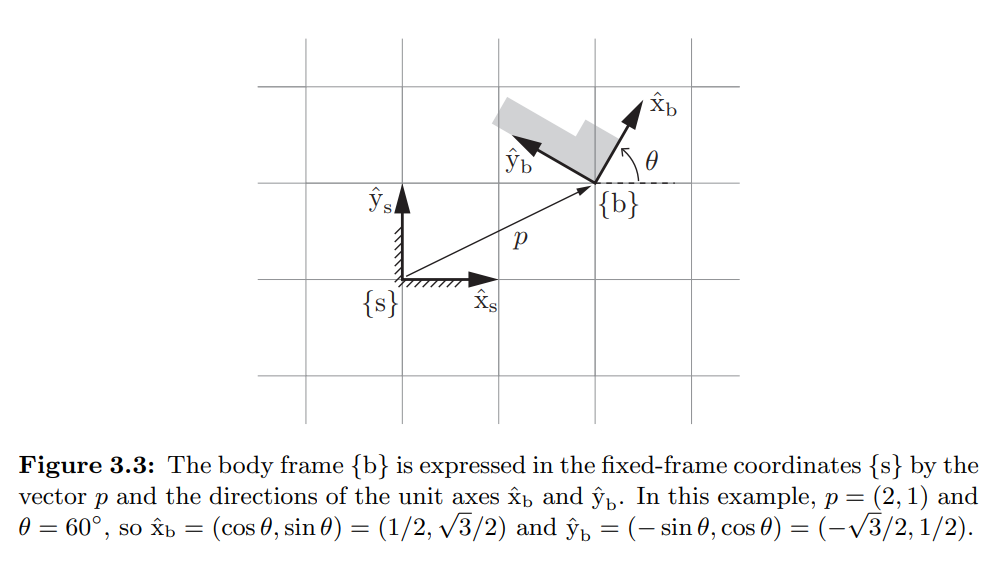
Figure 3.3에서 평면 몸체(회색 부분)를 봐봅시다.
그림에서처럼 단위축 $\hat{x}_s,\, \hat{y}_s$를 갖는 고정된 기준틀(reference frame) $\lbrace s \rbrace$이 있을 때 비슷하게 단위축 $\hat{x}_b,\, \hat{y}_b$를 갖는 평면몸체의 기준틀을 지정할 수 있습니다.(책에서 hat표기는 단위벡터를 의미합니다.)
그 틀을 body frame이라 하고 $\lbrace b \rbrace$로 표기합니다.
평면 몸체의 위치(position) 를 설명하기 위해서는 고정된 기준틀(fixed frame)에 대한 몸체의 위치(position)와 방향(orientation)만으로 충분합니다.
Figure 3.3에서 $\lbrace b \rbrace$의 원점인 $p$는 $\lbrace s \rbrace$의 좌표축을 이용해 다음과 같이 쓸 수 있습니다.
일반적으로 $p$벡터를 $p = (p_x,p_y)$로 표기하지만 이 방식은 기준틀(reference frame)이 모호해지는 단점이 있습니다.
따라서 식 3.1과 같이 표기해 $(p_x,p_y)$가 어떤 기준틀에서 정의되었는지 확실하게 명시할 수 있습니다.
다음으로 고정된 frame $\lbrace s \rbrace$에 대한 몸체의 frame $\lbrace b \rbrace$의 방향(orientation) 은 Figure 3.3에서 각 $\theta$를 통해 설명할 수 있습니다.
$\lbrace b \rbrace$의 단위 벡터 $\hat{x}_b ,\, \hat{y}_b$를 $\lbrace s \rbrace$의 그것들로 표현하면 다음과 같습니다.
$p$의 모든 성분을 $\lbrace s \rbrace$에 대해 쓰기로 하면 열벡터 $p \in \mathbb{R}^2$는
\[p = \begin{bmatrix} p_x \\ p_y \end{bmatrix}\]이고 두 벡터 $\hat{x}_b ,\, \hat{y}_b$또한 열벡터로 쓸 수 있기 때문에 이들을 모아 $2 \times 2$ 행렬 $P$로 쓰면 다음과 같습니다.
\(P = \begin{bmatrix} \hat{x}_b & \hat{y}_b \end{bmatrix} = \begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix}\)
행렬 $P$는 회전 행렬(rotation matrix) 의 한 예시입니다.
순서쌍 $(P,p)$는 $\lbrace s \rbrace$에 대한 $\lbrace b \rbrace$의 방향과 위치에 대한 정보입니다.
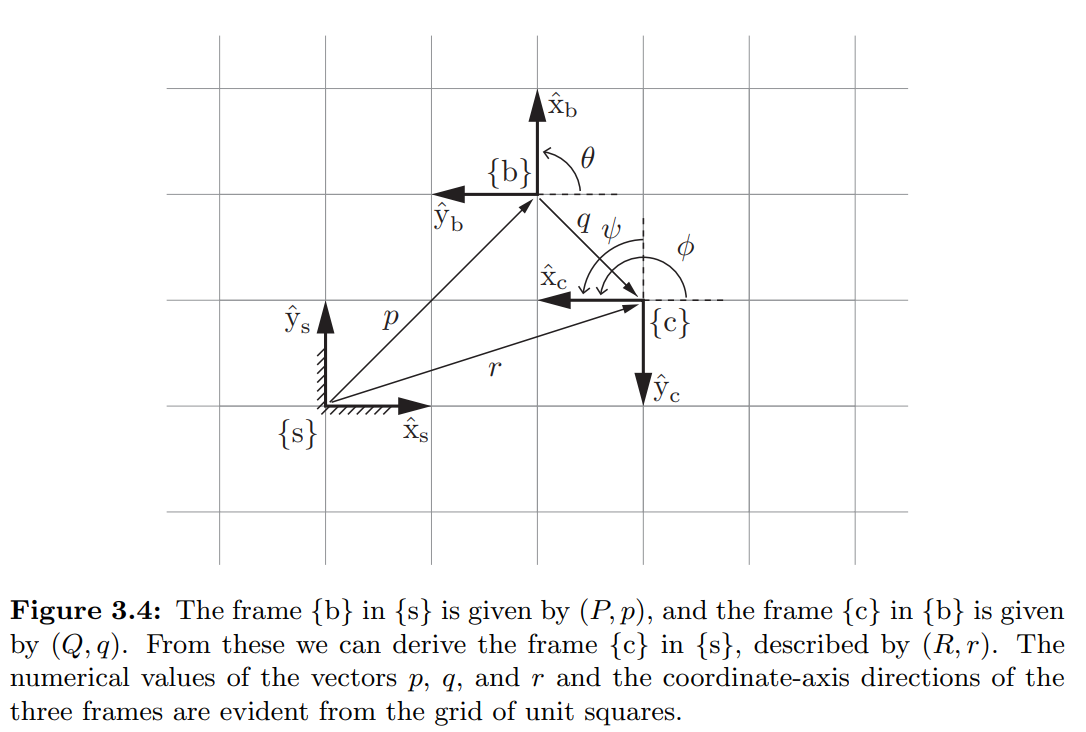
Figure 3.4에 있는 3개의 frame을 봅시다.
위의 방식을 똑같이 적용하면 다음과 같은 $\lbrace s \rbrace$에 대한 $\lbrace c \rbrace$의 정보인 순서쌍 $(R,r)$을 얻을 수 있습니다.
또 frame $\lbrace c \rbrace$를 $\lbrace b \rbrace$에 대해 쓸 수 있습니다.
$q$를 $\lbrace b \rbrace$의 좌표로 표현된 $\lbrace b \rbrace$의 원점으로부터 $\lbrace c \rbrace$의 원점까지의 벡터라 하고, $Q$를 $\lbrace b \rbrace$에 대한 $\lbrace c \rbrace$의 방향(orientation)이라 하면 다음과 같은 순서쌍 $(Q,q)$를 얻을 수 있습니다.
$(Q,q)$ ($\lbrace b \rbrace$에 대한 $\lbrace c \rbrace$의 위치)와 $(P,p)$ ($\lbrace s \rbrace$에 대한 $\lbrace b \rbrace$의 위치)를 알고 있다면, 다음과 같이 $\lbrace s \rbrace$에 대한 $\lbrace c \rbrace$의 위치를 계산해낼 수 있습니다.
\(R = PQ \tag{3.8}\)
\(r = Pq + p \tag{3.9}\)
식(3.8)은 $Q$를 $\lbrace s \rbrace$ frame에 대한 것으로 변환한 것이고,
식(3.9)는 $q$를 $\lbrace s \rbrace$ frame에 대해 변환하고 $p$와 벡터합 한 것입니다.
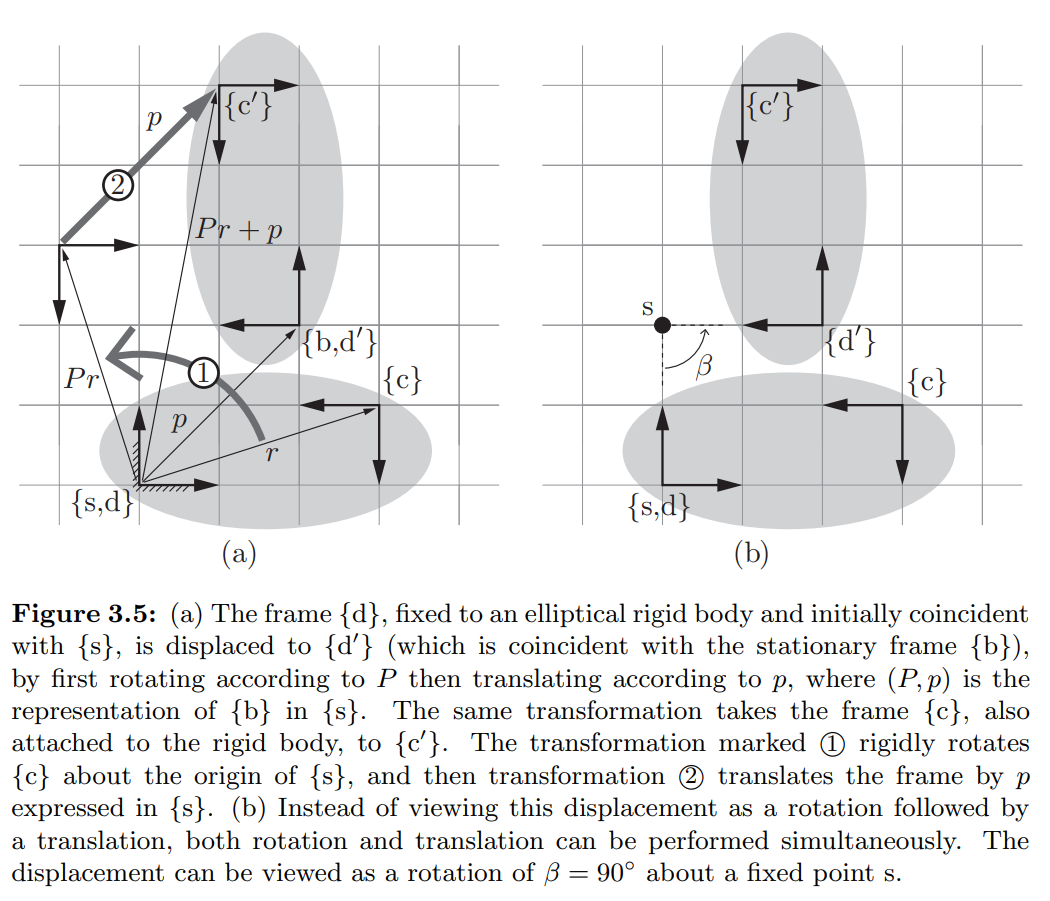
두개의 frame $\lbrace d \rbrace, \lbrace c \rbrace$이 붙어있는 강체(rigid body)에 대해 생각해봅시다.
$\lbrace d \rbrace$는 초기에 $\lbrace s \rbrace$와 동일한 위치에 있고, $\lbrace c \rbrace$는 $\lbrace s \rbrace$에 대해 $(R,r)$로 표현됩니다.
그리고 몸체가 움직여 $\lbrace d \rbrace$는 $\lbrace d’ \rbrace$으로 움직여 $\lbrace b \rbrace$ ($\lbrace s \rbrace$에 대해 $(P,p)$로 표현)와 일치하게 되었습니다.
이런 움직임 이후에 $\lbrace c \rbrace$는 어디로 위치하게 될지 알아봅시다.
$\lbrace c \rbrace$의 도착 위치를 $\lbrace c’ \rbrace$라 하고 이 frame의 위치를 $(R’,r’)$이라고 하면
\(R' = PR \tag{3.10}\)
\(r' = Pr + p \tag{3.11}\)
임을 알 수 있습니다.
따라서 회전 행렬-벡터 쌍 $(P,p)$은 3가지 용도로 활용이 가능합니다.
- 강체(rigid body)의 위치(configuration)을 표현하기 위해 [Figure 3.3]
- 벡터나 frame의 기준 frame (reference frame)을 바꾸기 위해 [Figure 3.4]
- 벡터나 frame을 이동(displace)시키기 위해 [Figure 3.5(a)]
Figure 3.5의 움직임은 강체가 ①만큼 회전하고 ②만큼 평행운동 한 것으로 해석이 가능하지만, 다르게 보면 단순히 점 $s$를 기준으로 $\beta$만큼 회전 한 것으로도 볼 수 있습니다.
이것은 하나의 평면 나사 운동(screw motion) 예시입니다.
이 움직임은 세개의 변수 $(\beta, s_x, s_y)$로 표현될 수 있습니다.
위의 예시에서는 $(s_x, s_y) = (0,2)$이겠군요.
screw motion을 표현하는 다른 방법은 motion을 회전과 직선 운동의 결합으로 표현하는 것입니다.
Figure 3.5(b)를 보면 점 s를 기준으로 단위 각속도 $(\omega = 1\, rad/s)$ 만큼 회전하는 운동은 초기에 {$s$}의 원점이 {$s$} frame의 $+\hat{x}$방향으로 초당 2만큼 움직인다는 것을 알 수 있습니다. ($(v_x, v_y) = (2,0)$)
이상을 하나의 screw axis인 벡터$S$로 표현하면
\(S = (\omega, v_x, v_y) = (1, 2, 0)\)
입니다.
$S$를 따라 $\theta \over 2$만큼 이동하면 최종 지점에 도달합니다. 따라서 이 운동(움직임)을 $S\theta = (\pi/2, \pi, 0)$으로 표현할 수 있고 이것을 평면 강체의 움직임에 대한 exponential coordinates라고 합니다.
3.2 Rotations and Angular Velocities
3.2.1 Rotation Matrices (회전 행렬)
회전 행렬 $R$의 열들은 각각 body-frame의 단위 축(unit axes) $\lbrace\hat{x}_b,\hat{y}_b,\hat{z}_b\rbrace$입니다.
따라서 다음이 성립합니다.
(a) $\hat{x}_b,\hat{y}_b,\hat{z}_b$가 모두 단위벡터 이므로
\(r_{11}^2 + r_{21}^2 + r_{31}^2 = 1
\\
r_{12}^2 + r_{22}^2 + r_{32}^2 = 1,
\\
r_{13}^2 + r_{23}^2 + r_{33}^2 = 1.
\tag{3.17}\)
(b) 각 벡터의 내적이 0 이므로 ($\hat{x}_b \cdot \hat{y}_b = \hat{x}_b \cdot \hat{z}_b = \hat{y}_b \cdot \hat{z}_b = 0$)
\(r_{11}r_{12} + r_{21}r_{22} + r_{31}r_{32} = 0,
\\
r_{12}r_{13} + r_{22}r_{23} + r_{32}r_{33} = 0,
\\
r_{11}r_{13} + r_{21}r_{23} + r_{31}r_{33} = 0.
\tag{3.18}\)
이상의 두 식을 다음과 같이 쓸 수 있습니다.
\[R^{T}R = I\]또 frame은 오른손 법칙을 따르기 때문에 (i.e., $\hat{x}_b \times \hat{y}_b = \hat{z}_b$) 행렬식(determinant)를 이용해 해당 constraint를 추가할 수 있습니다.
\[det R = {\hat{x}_b}^{T}(\hat{y}_b \times \hat{z}_b) = {\hat{z}_b}^{T}(\hat{x}_b \times \hat{y}_b) = {\hat{y}_b}^{T}(\hat{z}_b \times \hat{x}_b) = 1.\]3 $\times$ 3 회전 행렬은 special orthogonal group SO(3)의 형태입니다.
SO(3)는 (i) $R^{T}R=I$ 와 (ii) det$R = 1$ 을 만족하는 3 $\times$ 3 실수 회전 행렬을 뜻합니다.
추가로 SO(2)는 (i) $R^{T}R=I$ 와 (ii) det$R = 1$ 을 만족하는 2 $\times$ 2 실수 회전 행렬로 정의에 의해 다음과 같이 쓸 수 있습니다.
3.2.1.1 Properties of Rotation Matrices(회전 행렬의 성질)
회전행렬은 다음과 같은 성질을 갖습니다.
- 회전 행렬의 역행렬은 본래의 전치행렬과 같다. ($R^{-1} = R^{T}$)
- 두 회전 행렬의 곱은 회전 행렬이다. ($R_1,\, R_2 \in SO(3),\, R_1R_2 \in SO(3)$)
- 회전 행렬의 곱은 교환 법칙이 성립한다. ($(R_1 R_2)R_3 = R_1 (R_2 R_3)$)
3.2.1.2 Uses of Rotation Matrices(회전 행렬의 사용)
식 (3.10), (3.11)에서 본 것 같이 회전 행렬 $R$은 보통 다음 3가지의 의미로 사용합니다.
- 방향을 표현하기 위해
- 벡터나 frame이 표현된 reference frame(기준 frame)을 바꾸기 위해
- 벡터나 frame을 회전시키기 위해
첫번째처럼 쓰인다면 $R$은 frame을 표현하는 것으로 여겨지고, 두번째와 세번째처럼 쓰인다면 $R$은 벡터나 frame에 작용하는 연산자로 여겨집니다.

Figure 3.7은 동일한 지점에 있는 점 p와 각기 다른 3개의 frame을 보여줍니다. fixed space frame $\lbrace s \rbrace$는 $\lbrace a \rbrace$와 동일합니다.
$\lbrace s \rbrace$에 대한 각 frame들의 방향은 다음과 같습니다.
각 frame에서 p의 좌표는 다음과 같습니다.
\(\begin{aligned}
p_a = \begin{bmatrix}
1 \\
1 \\
0
\end{bmatrix}
,
p_b = \begin{bmatrix}
1 \\
-1 \\
0
\end{bmatrix}
,
p_c = \begin{bmatrix}
0 \\
-1 \\
-1
\end{bmatrix}
.
\end{aligned}\)
1. Representing an orientation(방향의 표현)
암묵적으로 $R_c$는 frame $\lbrace s \rbrace$에 대한 $\lbrace c \rbrace$의 방향입니다. 이를 좀 더 명시적으로 쓰면 $R_{sc}$로 쓸 수 있고 이 또한 동일한 뜻을 의미합니다. 이러한 방식은 어떤 한 frame을 $\lbrace s \rbrace$가 아닌 다른 frame에 대해 표현할 때 용이합니다. 예를 들어 $R_{bc}$는 $\lbrace b \rbrace$에 대한 $\lbrace c \rbrace$의 방향을 뜻합니다. frame에 대해 혼동할 여지가 없으면 단순히 $R$로 쓰기도 합니다.
Figure 3.7에서 다음을 알 수 있습니다.
단순 계산을 통해 $R_{ac}R_{ca} = I$임을 알 수 있고 따라서 $R_{ac} = R_{ca}^{-1}$ 입니다. 또는 회전 행렬의 첫번째 성질을 통해 $R_{ac} = {R_{ca}}^{T}$임을 알 수 있습니다.
두 frame $\lbrace d \rbrace$와 $\lbrace e \rbrace$에 대해 다음이 성립합니다.
2. Changing the reference frame(기준 frame의 변환)
회전 행렬 $R_{ab}$는 $\lbrace a \rbrace$에 대한 $\lbrace b \rbrace$의 방향을 나타내고, $R_{bc}$는 $\lbrace b \rbrace$에 대한 $\lbrace c \rbrace$의 방향을 나타냅니다. 간단한 계산으로 $\lbrace a \rbrace$에 대한 $\lbrace c \rbrace$의 방향이 다음과 같음을 알 수 있습니다.
위 식에서 $R_{bc}$는 $\lbrace c \rbrace$의 방향을 나타내는 것으로, $R_{ab}$는 기준 frame을 $\lbrace b \rbrace$에서 $\lbrace a \rbrace$로 바꾸는 연산자(operator)로 볼 수 있습니다.
첫 번째 행렬의 두번째 아래첨자와 두 번째 행렬의 첫번째 아래첨자(위 예시에서는 ‘b’)가 같으면 reference frame의 변환이 가능하다고 생각하면 기억하기 편리합니다.
마찬가지로 $\lbrace b \rbrace$에 대해 표현된 벡터 $p_b$를 $\lbrace a \rbrace$에 대해 표현되도록 할 수 있습니다.
\[R_{ab}p_b = p_a\]3. Rotating a vector or a frame(벡터나 frame의 회전)
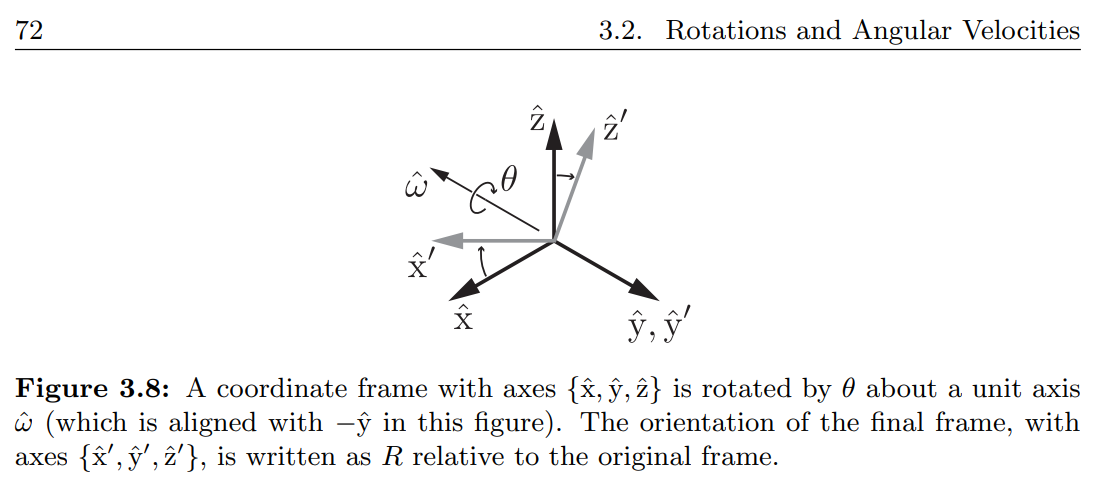
Figure 3.8에서 진한 부분은 $\lbrace \hat{x}, \hat{y}, \hat{z} \rbrace$을 축으로 하는 frame $\lbrace c \rbrace$ (=$\lbrace s \rbrace$) 입니다. 여기서 $\lbrace c \rbrace$를 단위축 $\hat{\omega}$를 중심으로 $\theta$만큼 회전하면 회색 부분인 $\lbrace \hat{x}’, \hat{y}’, \hat{z}’ \rbrace$을 축으로 하는 frame $\lbrace c’ \rbrace$을 얻습니다.
회전 행렬 $R = R_{sc’}$ 은 $\lbrace s \rbrace$에 대한 $\lbrace c’ \rbrace$의 방향이지만 다르게 생각해보면 $\lbrace s \rbrace$을 $\lbrace c’ \rbrace$으로 변환하는 역할을 한다고 볼 수 있습니다.
방향을 나타내는 것이 아닌 회전 연산자로써 $R$을 다음과 같이 쓸 수 있습니다.
\(R = Rot(\hat{\omega}, \theta)\)
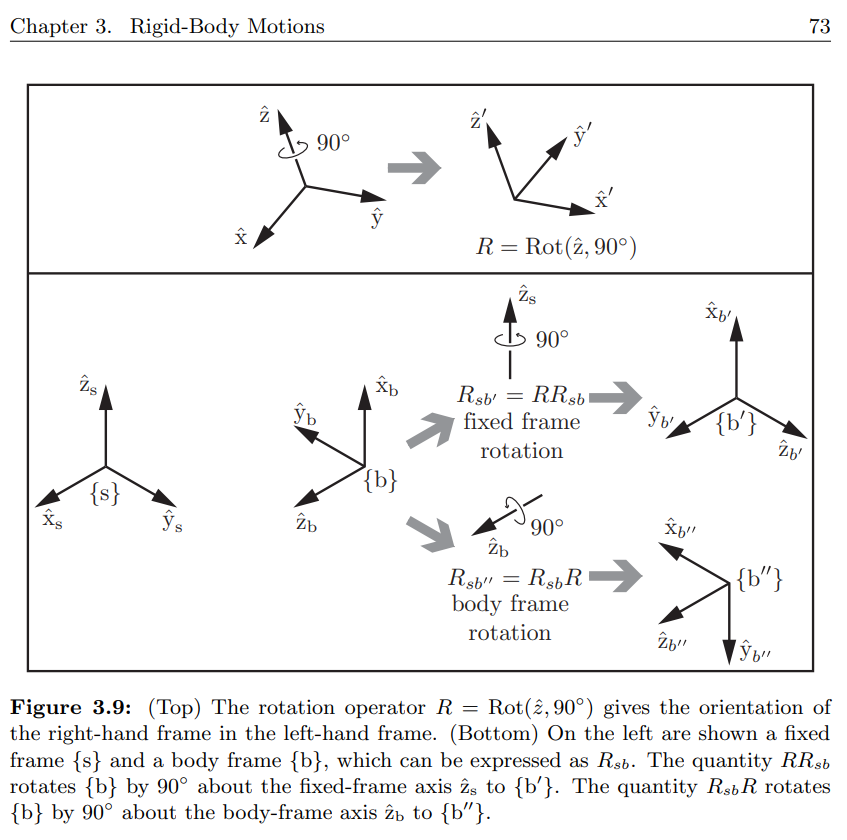
이제 $R_{sb}$가 $\lbrace s \rbrace$에 대한 $\lbrace b \rbrace$의 방향을 나타내고, $\lbrace b \rbrace$를 단위 축 $\hat{\omega}$을 중심으로 $\theta$만큼 회전시킨다고 생각해 봅시다($R = Rot(\hat{\omega}, \theta)$).
의미를 정확히 하기 위해 $\hat{\omega}$이 $\lbrace s \rbrace$ 좌표로 표현되었는지 $\lbrace b \rbrace$ 좌표로 표현되었는지 정해야 합니다. $\lbrace s \rbrace$와 $\lbrace b \rbrace$가 일치하지 않는 한, 이 선택에 따라 똑같은 값인 $\hat{\omega}$이라 할지라도 다른 결과를 가져올 수 있습니다.
$\lbrace b’ \rbrace$을 $\hat{\omega_s}$($\lbrace s \rbrace$에서 표현된 $\hat{\omega}$)에 대해 $\theta$만큼 회전했을 때의 frame이라 하고, $\lbrace b’’ \rbrace$을 $\hat{\omega_b}$($\lbrace b \rbrace$에서 표현된 $\hat{\omega}$)에 대해 $\theta$만큼 회전했을 때의 frame이라 하면 새로운 frame들은 다음과 같이 계산할 수 있습니다.
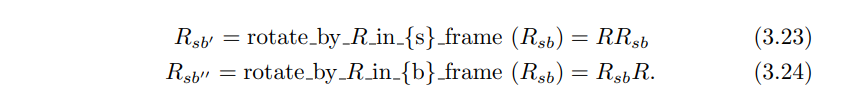
다른 말로 하면, $R = Rot(\hat{\omega}, \theta)$을 앞에 곱하면 $\hat{\omega}$이 fixed frame에서 표현된 것임을 뜻하고 뒤에 곱하면 $\hat{\omega}$이 body frame에서 표현된 것임을 뜻합니다.
